はじめに
この記事ではシュレディンガー方程式から固有エネルギーという量を導く出しました。固有エネルギーはミクロな世界での重要な量で光との相互作用や電流などを考えるときに有効な物理量でした。一方、この記事ではエネルギーの学問である熱力学を紹介しています。熱力学では物質はエネルギーが低いかつエントロピーは大きくなる方向へ遷移するという性質を紹介しました。そこで、今回は両者を結ぶ統計力学という分野を紹介したいと思います。統計力学を学び始めた方はややとっつきにくい分野かと思いますので、イメージを駆使して理解の助けにしたいと思います。また、具体的に式を計算し、熱力学との関係を理解していきましょう。その時に使った計算するプログラムも別の記事で紹介しますので自分でいろいろ試してみることでさらに理解が進めてみましょう。今回は固有エネルギーから確率分布まで解説します。
量子力学から熱力学へ
統計力学のイメージ
統計力学をイメージしてもらうために身近な例から始めます。シュレディンガー方程式の記事でも説明したように人の感情に置き換えてみます。この記事での固有エネルギーは各感情の度合いと説明しています。怒りが3、楽しいが5、悲しいが2とかです。これは内面的な話だったのですが、外に出てくる感情はこれとは少し違う感情の方が多いかと思います。内面の感情と外面の感情を繋ぐのが統計力学だと思ってください(笑)。以下の図は感情の統計力学の概要です。
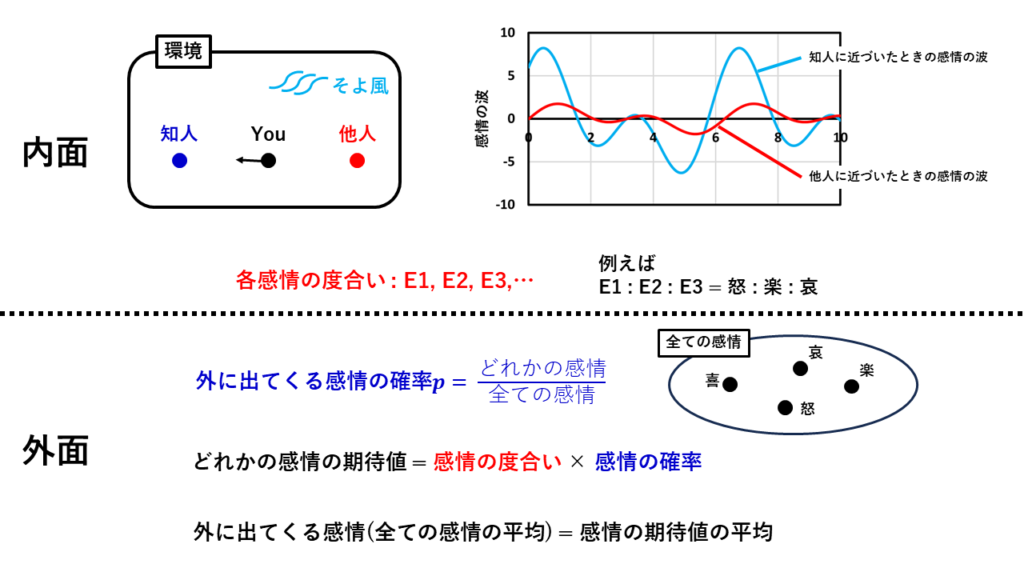
点線より上は固有エネルギーの説明でこの記事で説明しています。点線より下は今回説明する統計力学の概念です。最終的に求めたのは外に出てくる感情の量です。外に出てくる感情はいろいろな喜怒哀楽が混ざっています。どの喜怒哀楽がでてくるかの確率を表すために青字で示す式を定義します。式の意味はすべての感情のうち、どれかの感情の割合を示しています。例えば喜:怒:哀:楽=0.4:0.1:0.1:0.4などです。そして、その喜怒哀楽が出てくる期待値を2行目の式で定義します。楽しいが出てくる確率が高いなどです。最後に外に出てくる感情はすべての感情の期待値の平均です。ある環境に置かれたとき喜怒哀楽は色々混ざっていますが、その時に出てくる感情の度合いがその値です。
これが統計力学を感情に置き換えた時のイメージです。これを物理に変換していきます。
固有エネルギー
固有エネルギーは各感情の度合いでしたので、ある環境に置かれたときの各感情を計算します。これはこの記事で計算していますので、こちらを確認してみてください。今回は調和振動子型ポテンシャルで計算された結果を使います。感情で例えると、人に近づいたり離れたりしたときの環境(ポテンシャル)での感情(固有エネルギー)を求めているとしてください。固有エネルギーの式は以下のようになっています。
$$ E_n = \left(n+\displaystyle\frac{1}{2}\right)\hbar\omega $$
nは0~100で計算しています。このエネルギーを使って、各温度ごとの確率分布を求めていきます。予想としては、nが0に近いほど(エネルギーが小さいほど)確率が高くなりnが大きくなるにつれて小さくなると考えられます。また、温度が高くなるにつれ励起されn=0の確率が徐々に小さくなりnが大きいとろこの確率が増えると予想されます。
確率
まずは確率ですので、なにがでる確率か決めておきます。感情の話では「喜怒哀楽のどれかがでる確率」ですし、物理ですと「あるエネルギーがでる確率」になります。あるエネルギーというのは上の固有エネルギーだとn=0のときのエネルギー、n=1のときのエネルギーなどです。この確率pnは
$$ p_n = \frac{Z_n}{Z} $$
と定義されます。これは(あるエネルギーが値)/(すべてのエネルギーの値の和)となり、確率の定義そのままです。ただ、ZnとZは普通の確率で使われるようなPとかCではなく、以下のような式で定義されています。
$$ Z_n = \exp\left(-\frac{E_n}{k_BT}\right) $$
$$ Z = \displaystyle\sum_{n=0}^{100}Z_n $$
kBはボルツマン定数で1.38×10^(-23)(^は10の肩に乗って何乗を示します。)です。Tは温度です。これをnとTの関数として計算し、グラフにしてみます。
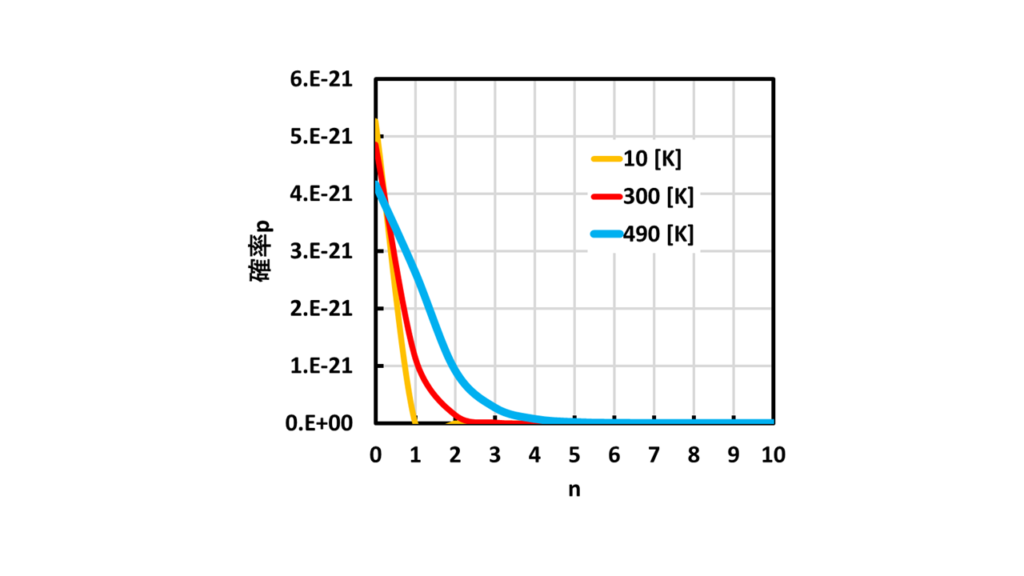
横軸にn、縦軸に確率を示しています。各グラフの色は温度を示しています。どの温度でもnが大きくなるにつれ確率が小さくなり、最終的には0になっています。これは直観的にも合致していてn=0は基底状態なので、その状態をとる確率が高くなり、n>0では励起状態なので周囲からエネルギーをもらわない限りその状態での確率は小さくなることになります。また、温度が徐々に高くなると熱エネルギーを得て、励起状態をとることができnが大きいところでも確率が増えてきます。
では次回、この確率分布から熱力学に登場する内部エネルギーと結び付けましょう。
最後に
このように固有エネルギーからその状態をとる確率を求めることができます。しかも直観的に一致するような結果も得られます。参考書に書かれているような式がきちんと直感に合う形で理解することができました。ここでは調和振動子の固有エネルギーだけと取り上げましたが、コードも公開するので、それ以外の固有エネルギーの分布でも試してみて理解を深めましょう。


コメント