はじめに
本記事は
3.2. 【例題】量子非調和振動子の固有状態
こちらを参考、一部コードの引用をおこなっております。
詳しい説明はこちらをご確認お願いします。
本記事ではコードの「ここがすごい」や「これは参考になる」と思ったところを紹介します。
また、なぜそう思ったかを説明します。
コード
やりたいこと
任意のポテンシャル関数における波動関数の挙動及び固有値を求める。
ポテンシャルの違いで波動関数の挙動の変化を確認する。また、そのときの固有値からどんなことが考えられるか。
今回のプログラミングポイント
pythonでの数値計算
その他ポイント
自分のブログの参考ページ
今回のコード
import numpy as np
from scipy import linalg
import pandas as pd
def make_second_deriv(dim, dx):
I = np.identity(dim, dtype=int)
M = np.roll(I, 1, axis=1)
M_t = M.transpose()
K = (-2.0 * I + M + M_t) / (dx*dx)
return K
def solve_anharmonic(x_max, nx, anharmonicity, n_vec=10):
print("making Hamiltonian...")
# arrays containing x, x^2, x^4
x = np.linspace(-x_max, x_max, 2*nx)
x2 = x**2 # element-wise square
x4 = x2**2
x6 = x2**3
dx = x[1] - x[0]
print("dx =", dx)
# potential term
v_diag = 0.5 * x2 + anharmonicity * x4 + anharmonicity * x6
v_matrix = np.diag(v_diag)
# kinetic term, -(1/2) d^2/dx^2
kin_matrix = -0.5 * make_second_deriv(2*nx, dx)
# Hamiltonian
h_matrix = v_matrix + kin_matrix
# diagonalize
print("diagonalizing Hamiltonian...")
eigval, eigvec = linalg.eigh(h_matrix)
# normalize eigenvectors so that the result does not depend on dx
eigvec /= np.sqrt(dx)
eigvec = np.abs(eigvec)**2
# save result for eigenvalues
print("saving results...")
df_x = pd.DataFrame(x)
df0 = pd.DataFrame(v_diag)
df1 = pd.DataFrame(eigval)
df2 = pd.DataFrame(eigvec)
df2 = pd.concat([df_x, df0, df2], axis=1)
df1.to_csv("koyuuti.csv")
df2.to_csv("hadoukannsuu.csv", index=None)
return eigval, eigvec
def main():
nx = 100
x_max = 10
anharmonicity = 0.25
solve_anharmonic(x_max, nx, anharmonicity)
if __name__ == '__main__':
main()解説
背景
まず、どうして任意のポテンシャルの波動関数と固有値を解析するのか?
経緯としては以下のような研究例があります。
アンモニア反転運動の実空間観測に向けて
アンモニアの反転振動は状態1からポテンシャルを乗り越えて状態2に遷移します。その挙動を詳細に解析するにはシュレディンガー方程式を解いて、波動関数の挙動を確認しなければならなりません。よって、今回のようなプログラムで挙動を確認することにしました。
そのため、コードにはシュレディンガー方程式を作って、計算をするということを反映させなければならなりません。今回はシュレディンガー方程式を作るに重点を置いて説明したいと思います。
シュレディンガー方程式の形は
$$(K + V)\Psi = E \Psi$$
となります。Kは運動エネルギー、Vはポテンシャルエネルギー、Eは固有エネルギー、ψは波動関数です。今回のプログラムではVがインプットでE、ψがアウトプットとなります。
これをコードに反映させていきたいと思います。この式をコードに反映させるために以下のような変換を行います。
シュレーディンガー方程式を行列風に描く
通常、Kは微分ですが、コードに反映させやすいように行列に変換しています。これができるのはシュレディンガー方程式が固有方程式と類似した”形”だからです。(私はこのことを知ったときは少し感動しました。紹介できる記事を書きます。)
解説
この変換のおかげでようやくコードに書き記していきます。しかし、Kの行列を作るのは難しそうです。今回紹介したコードはこれを簡単に作成していたので、その部分をピックアップします。
その前に私が持っているイメージを紹介します。
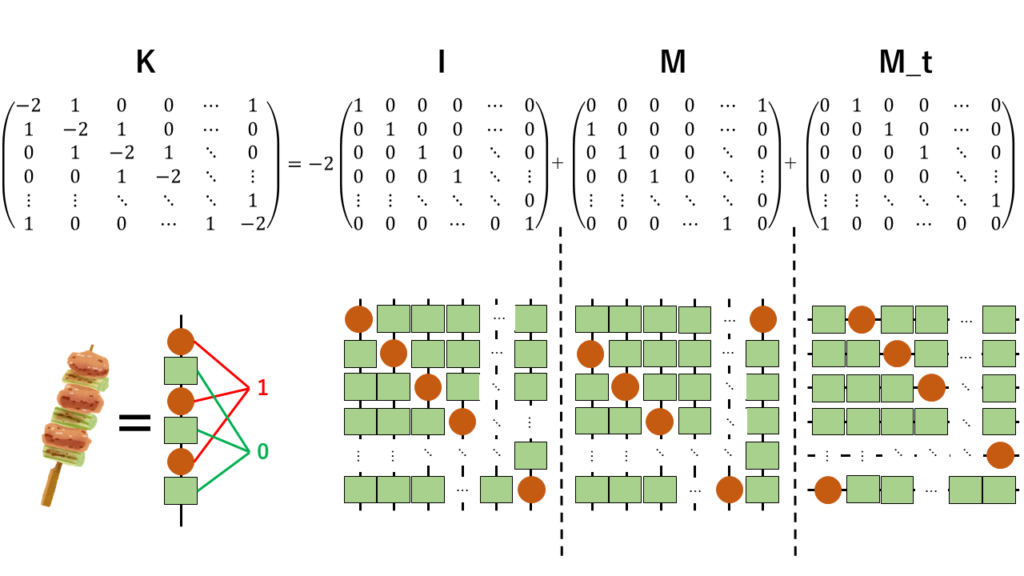
Kは数学の知識を使って上記のように3つ行列に分解できます。そして、それぞれにI、M、M_tと名前をつけます。I、M、M_tを焼き鳥でイメージしてみましょう(笑)。1を鶏肉、0をねぎとするとねぎまができあがります。各行列の縦方向に串を通して、焼き鳥串の出来上がりです。そのようにイメージすると各行列の各串に1つだけ鶏肉がついて、あとはネギだけというダイエットに最適な焼き鳥の完成です。イメージの準備はここまでです。ここからがすごいところです。MとM_tはIの鶏肉とネギを少し移動しただけで作ることができます。その操作を以下に示します。

まず、Iの取っ手側のお肉とネギをとって、食べる側の串先に刺しなおします。すると1行下に移動します。これでIがMに変換されます。次にMになった串たちの取っ手側をすべて持ち、反時計回りに回転させて裏表ひっくり返します。イメージとしては右手の指の間に串を持ち、手首を手前から奥に持ち上げるように手のひらをひっくり返ようにする感じです。すると、MがM_tに変換されます。これでIからM、M_tを作り出すことができました。あとはKに戻すために-2×I+M+M_tという演算します。これをコードに反映させます。
def make_second_deriv(dim, dx):
I = np.identity(dim, dtype=int)
M = np.roll(I, 1, axis=1)
M_t = M.transpose()
K = (-2.0 * I + M + M_t) / (dx*dx)
return K上記関数(make_second_deriv)のうちIがdim×dimの単位行列です。MがIを1行下にずらしています。M_tがMを転置させています。そして、最後にKを計算しています。
最後に
このコードを初めて見たとき、とても感動しました。これを知る前の私であればIからMを作り出そうとは思いませんでした。1行移動するというコマンドは知っていましたが、このような発想で作ろうと思いませんでした。
今回はここまでになります。
今回のような発想がすぐ思いつくようこれからも精進していきたいと思います。
次回はこのプログラムを使ってポテンシャルによって波動関数の挙動や固有値を解析してみます。量子力学の初学者さんや解析の流れなど見たい方はそちらもよろしくお願いします。
2023/08/02 J.A


コメント