はじめに
前回まではミクロの観点(固有エネルギーの確率分布)からマクロの観点な量(内部エネルギー)を導出しました。内部エネルギーを使って実際の物質を理解したり議論したりするのはやや難しいです。内部エネルギーは原子や分子の運動エネルギーとポテンシャルエネルギーの平均なので、その物質の状態が安定化どうかというのは内部エネルギーでは分かりません。そこで、内部エネルギーよりも扱いやすい自由エネルギーという量を導出したいと思います。自由エネルギーの詳しい説明はこちらの記事を参考にしてください。また、エントロピーも導出し、直観的な感覚と比較していきたいと思います。
自由エネルギー
まずは自由エネルギーを導出しますが、一般的な式変形などは参考書やこちらのような記事などを参考にしてください。
自由エネルギーをFとし、固有エネルギーを確率で重みづけして足したもの(分配関数)をZとすると以下のような式が成り立ちます。
$$ F = -k_BT\ln Z $$
kBはボルツマン定数で、Tは温度です。
さて、この式を使ってプログラムを作成し、直観的な感覚と比較してみましょう。
そこで前回求めたZを使って、各温度毎のFを算出します。横軸に温度、縦軸に自由エネルギーFをプロットします。
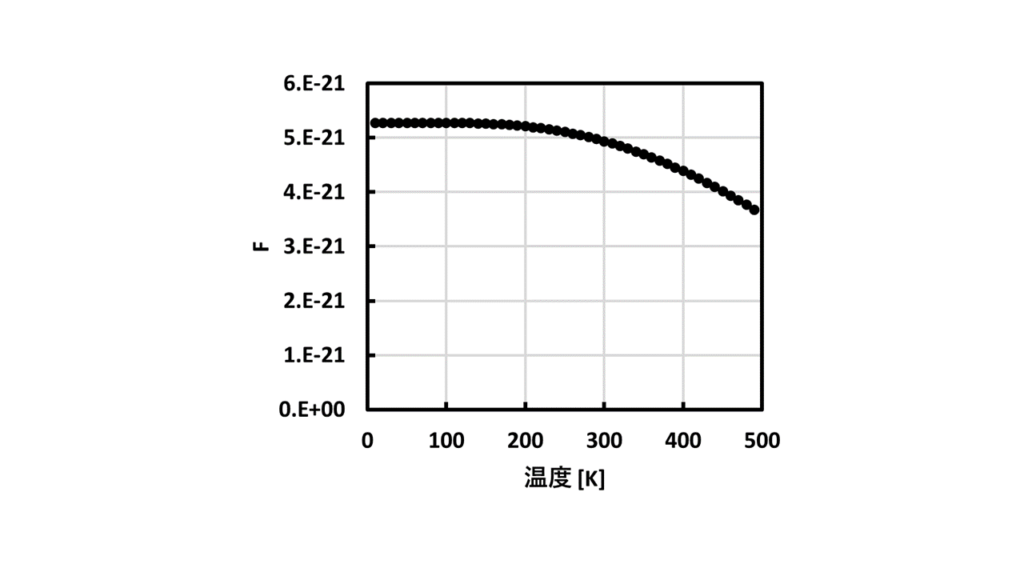
温度が上昇すると、自由エネルギーFは徐々に小さくなっていきます。自由エネルギーが小さくなるといことはより安定な状態になるということを示しています。しかし、直観的には温度が低いときの方が安定なはずです。
また、前回の内部エネルギーUでは温度が低いときの方が内部エネルギーが低くなっています。内部エネルギーと自由エネルギーとで矛盾が生じているように思えます。
実は自由エネルギーは内部エネルギーとエントロピーの2つの因子で変化することが分かっています。そこで、自由エネルギーが低くなる条件というものは内部エネルギーが低くなるかエントロピーが増加するかになってきます。詳しくはこちら。
なので、今回の自由エネルギーが温度で増加することを考察するにはエントロピーも計算しなければなりません。次にエントロピーを求めてみましょう。
エントロピー
エントロピーは自由エネルギーと内部エネルギーから逆算してみましょう。本来は状態数からボルツマンの原理を用いて導出すべきですが、今回は簡易的に導出します。
エントロピーSは自由エネルギーF、内部エネルギーUを使って
$$ S = \displaystyle \frac{U-F}{T} $$
で求められます。これを使って、横軸に温度、縦軸にエントロピーSをプロットすると
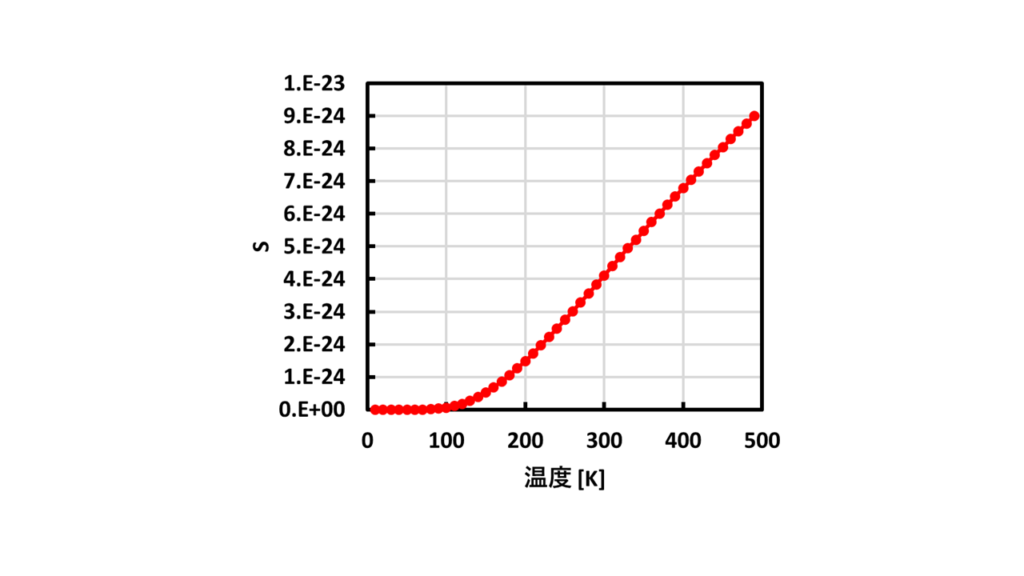
のようになります。温度が上昇する毎にエントロピーが大きくなっていくことが分かります。これは直観的にも一致します。温度が上昇すると原子や分子はより乱雑になる方向に遷移していきますので、乱雑さを示すエントロピーが増えていきます。
自由エネルギーが温度上昇で減少したのは内部エネルギーの効果よりもエントロピーの効果が強くなったと考えられます。
最後に
今回の系は調和振動子という単純な系で行っているので、考察ができました。しかし、より複雑な系になったとき自由エネルギーが最小になる条件の考察は困難になります。複雑な系を理解するためにはシミュレーションなどの活用が必要になってきます。例えば、こちらの記事などです。より本格的に行うために趣味で研究しています(笑)。


コメント