計算グラフと順伝播について調査してみた。(初心者が本とChatGPTを使ってAIを作って研究してみた）

はじめに

これまでChatGPTやネットを使ってAIの数字分類や回帰について調査してきました。

なんとなく、AIでできることや概要が分かるようになってきましたので、次にどうやってAIが動いているのか本とChatGPTを使って調査していきたいと思います。

今回は計算グラフと順伝播について調査していきたいと思います。

参考にした本は

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装 [ 斎藤 康毅 ] 価格：3,740円（税込、送料無料) (2024/2/19時点) 楽天で購入

順伝播を勉強してみた

計算グラフ

計算グラフというのはAIの原理、特にモデルを視覚的に分かりやすくしたものらしく以下の図のようによく見る図が計算グラフのようです。

計算グラフは〇で描いたニューロンとニューロンとニューロンが結合された線で構成させています。また、入力層と出力層が必ず存在し、その間を中間層や隠れ層と言われているようです。

計算グラフは視覚的にも分かりやすいのは特徴ですが、実際に計算するときにも活用できるようです。

上記、参考にした本ではすごく具体的で分かりやすい解説がありましたが、私の方では実際のmnistで自分が理解した範囲で説明してみたいと思います。

まずはmnistとはこちらで調査しましたので、参考にしてください。

mnistは数字画像ですが、1つの数字に対して28×28の数が割り振られており、それが60000枚あります。それをExcelなどで見ると以下の図の上のようなデータになります。

各行に1つの画像データを平坦化したものが並んでおり、60000行あります。

これを計算グラフの入力層にセットします。下図のExcelの下に計算グラフを書きました。入力層は28×28の784個のニューロンになりますが、すべて書くのが大変だったので10個書いています。

その入力層から隠れ層の2個のニューロンに結合され、最後に0~9を判別するための10個のニューロンからなる出力層があります。

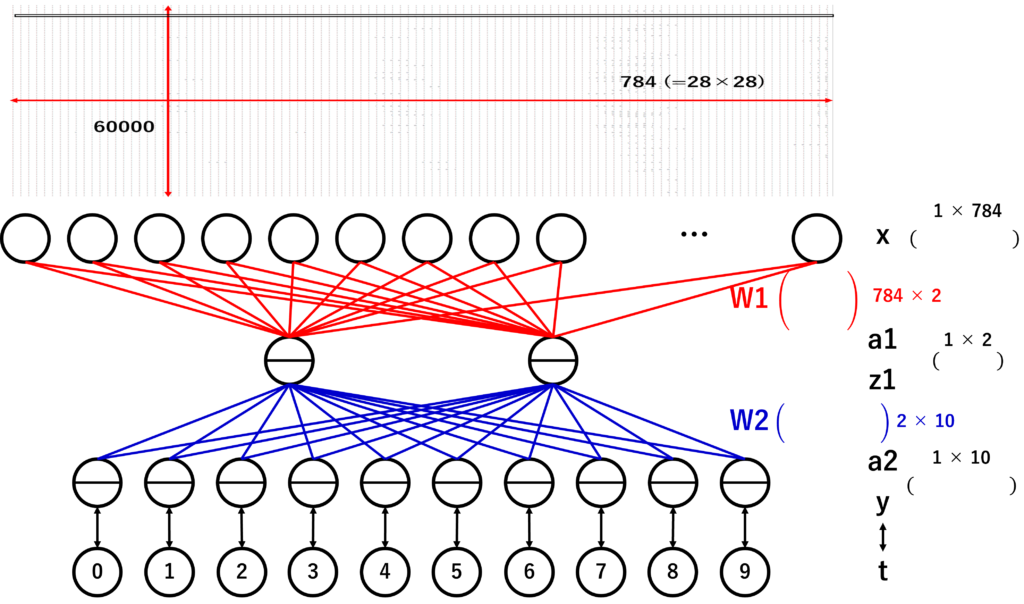
各層を数学の行列で表し、行列の各要素をニューロンの値に対応させると便利に計算できるようなので、入力層を1×784の行列、隠れ層を1×2の行列、出力層を1×10の行列とします。1は本来データの個数(mnistだと60000個)なのですが、Excelの1行だけ処理した場合を想定しています。そして、784、2、10は各層のニューロンの個数に当たります。

ただ、入力層から隠れ層にデータを移すのにニューロンの数が合わないので、うまく移せないように感じますが、ここで、各ニューロン同士の結合の強さを表す行列を定義することでデータを移せそうです。

順伝播

そこで、1×784から1×2へ変換する行列は784×2になります。これをW1とします。次に1×2から1×10へ変換する行列は2×10になります。これをW2とします。W1とW2を使うと各層でデータを渡せそうです。

このデータを各層へ渡していくことを順伝播というようです。

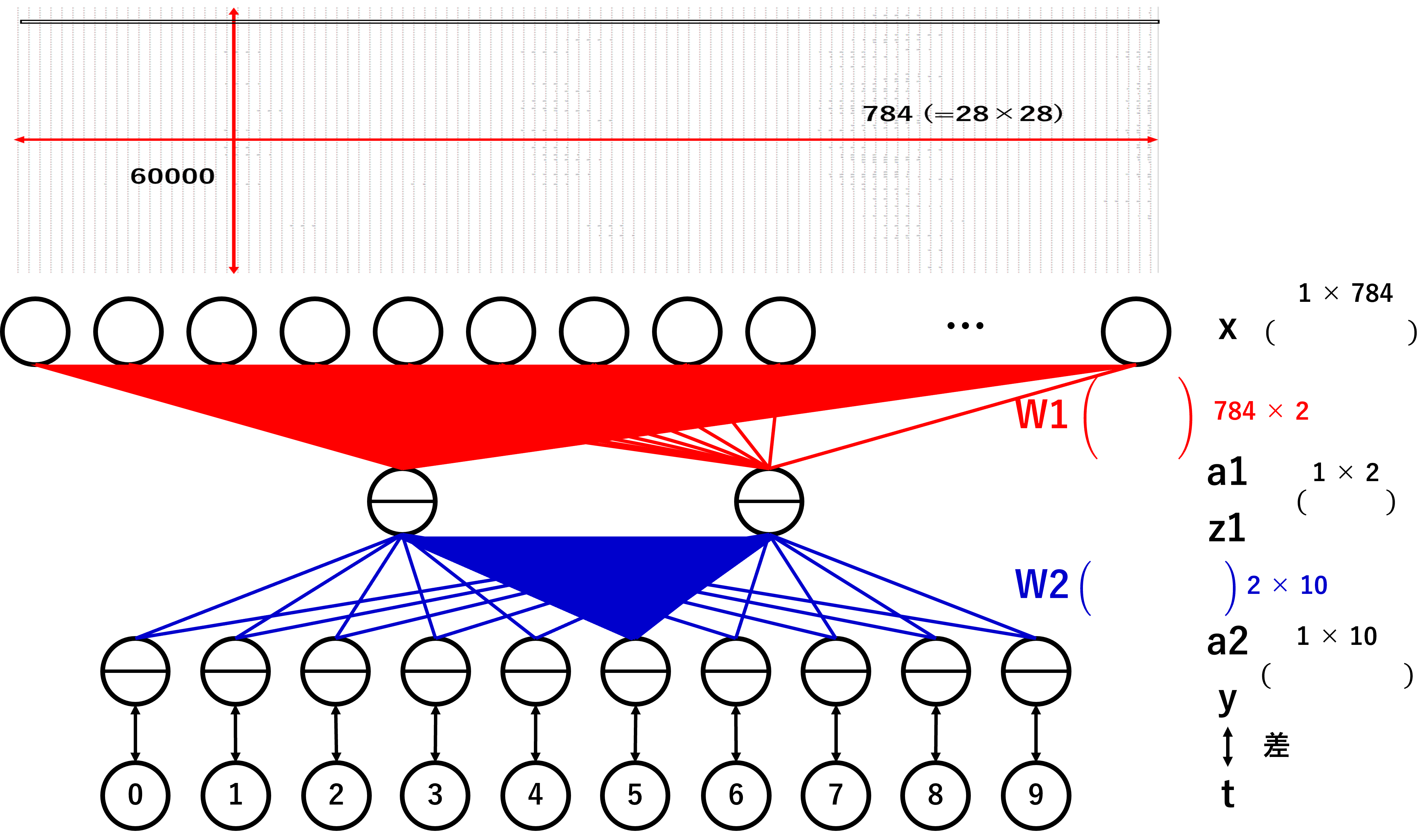
より具体的にデータを渡す流れを1つのニューロンに順伝播する様子を以下の図で示してみました。

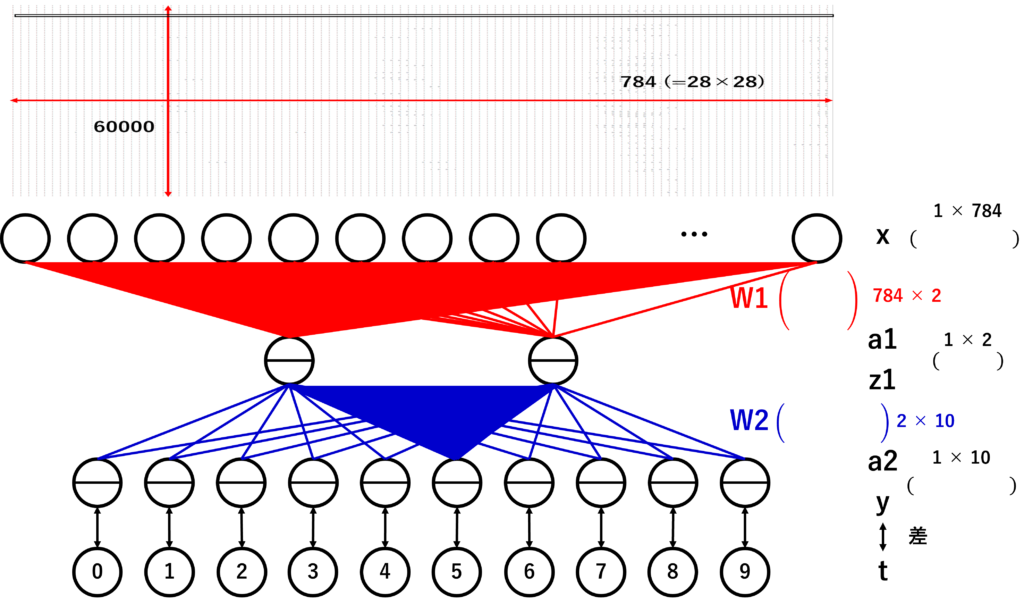
784個のニューロンから隠れ層の1つのニューロンへ伝播しています。そして、隠れ層の2から5番に該当するニューロンに伝播していきます。(う～ん。伝われ！)

順伝播を実装してみた

これをコードで自作してみます。(本をだいぶ参考にしています。)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical

(x_train, t_train), (x_test, t_test) = mnist.load_data()

x_train = x_train.reshape((x_train.shape[0], -1)).astype('float32') / 255
x_test = x_test.reshape((x_test.shape[0], -1)).astype('float32') / 255
t_train = to_categorical(t_train, 10)
t_test = to_categorical(t_test, 10)
 
input_size = 784
output_size = 10
 
hidden_size = 2
 
weight_init_std = 0.01
 
W1 = weight_init_std * np.random.randn(input_size, hidden_size)
b1 = np.zeros(hidden_size)
W2 = weight_init_std * np.random.randn(hidden_size, output_size)
b2 = np.zeros(output_size)
 
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
 
def softmax(x):
    x = x - np.max(x, axis=-1, keepdims=True)
    return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
 
x = x_train
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)

最後の5行で順伝播を行っています。単純なコードなのですべては解説しませんが、順伝播を行う上で必要な2点を解説します。

Wの値について

1つ目はWの値です。該当箇所は

W1 = weight_init_std * np.random.randn(input_size, hidden_size)
W2 = weight_init_std * np.random.randn(hidden_size, output_size)

です。np.random.randnは正規分布に従うようにランダムに数字を作っています。

決まった数字でもいいのですが、ランダムに作った方が実行するたびにyの値が変わって面白いです。

行列の積

2つ目は行列の積です。該当箇所は

a1 = np.dot(x, W1) + b1
a2 = np.dot(z1, W2) + b2

です。高校は大学で行列の積を計算した経験がある方は分かると思うのですが、普通の積とは違う計算をしなければなりません。しかも積の順を間違えると結果が変わってしまいます。

np.dotという関数で行列の積をすることができ、便利です。しかし、積の順は間違えないように設定しないと結果が異なってきますので、そこは注意が必要です。

これは慣れれば大したことないのですが、慣れるまでは紙に行列を書いて掛ける順を確認するといいかもしれません。

最後に

これでとりあえず、順伝播を実装することができました。

次回は順伝播の逆、逆伝播を行ってみたいと思います。