はじめに
これまでChatGPTやネットを使ってAIの数字分類や回帰について調査してきました。
なんとなく、AIでできることや概要が分かるようになってきましたので、次にどうやってAIが動いているのか本とChatGPTを使って調査していきたいと思います。
今回は順伝播と逆伝播を繰り返してAIの精度がどのように上がっていくのか重みと損失関数の履歴を追って調査してみたいと思います。
参考にした本は
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
順伝播と逆伝播を繰り返してみた
概要
前回までに順伝播と逆伝播という方法でAIが動いていることが分かりました。(順伝播に関してはこちら、逆伝播に関してはこちら)。しかし、すぐに精度の高いAIが作れるわけではなく、順伝播と逆伝播を繰り返して、各ニューロン同士の重みを適切な値にしなければならないということが分かりました。
そこで、今回は順伝播と逆伝播を繰り返して重みがどのように変化していくのか見ていきたいと思います。
また、逆伝播でも逆伝播誤差法を使うので、予測した数字と正解の数字の差(誤差関数)が更新するたびにどう変化するのかも確認してみたいと思います。
コード
では、まずコードを(コードの解説は前回までの記事を参考にしてみてください)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical
(x_train, t_train), (x_test, t_test) = mnist.load_data()
x_train = x_train.reshape((x_train.shape[0], -1)).astype('float32') / 255
x_test = x_test.reshape((x_test.shape[0], -1)).astype('float32') / 255
t_train = to_categorical(t_train, 10)
t_test = to_categorical(t_test, 10)
input_size = 784
output_size = 10
hidden_size = 50
weight_init_std = 0.01
W1 = weight_init_std * np.random.randn(input_size, hidden_size)
b1 = np.zeros(hidden_size)
W2 = weight_init_std * np.random.randn(hidden_size, output_size)
b2 = np.zeros(output_size)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def softmax(x):
x = x - np.max(x, axis=-1, keepdims=True)
return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
learning_rate = 0.1
x = x_train
t = t_train
W1_good_list = []
W1_notgood_list = []
W2_good_list = []
W2_notgood_list = []
MSE_list = []
for _ in range(10000):
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
dy = (y - t) / x.shape[0]
MSE = (1/x.shape[0]) * np.sum((t - y)**2)
MSE_list.append(MSE)
grad_W2 = np.dot(z1.T, dy)
grad_b2 = np.sum(dy, axis=0)
W2 = W2 - learning_rate * grad_W2
b2 = b2 - learning_rate * grad_b2
dz1 = np.dot(dy, W2.T)
da1 = sigmoid_grad(a1) * dz1
grad_W1 = np.dot(x.T, da1)
grad_b1 = np.sum(da1, axis=0)
W1 = W1 - learning_rate * grad_W1
b1 = b1 - learning_rate * grad_b1
W1_good = W1[235,0]
W1_notgood = W1[235,25]
W2_good = W2[0,5]
W2_notgood = W2[0,0]
W1_good_list.append(W1_good)
W1_notgood_list.append(W1_notgood)
W2_good_list.append(W2_good)
W2_notgood_list.append(W2_notgood)
print(_)
x = x_train
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
test_data = np.argmax(t, axis = 1)
pred_data = np.argmax(y, axis = 1)
error = np.sum(test_data == pred_data)
print(str(error) + " / " + str(x_train.shape[0]))
df = pd.DataFrame(list(zip(list(range(10000)), W1_good_list, W1_notgood_list, W2_good_list, W2_notgood_list)), columns=["iter", "W1_good", "W1_notgood", "W2_good", "W2_notgood"])
df.to_csv("dW.csv", index=None)
df2 = pd.DataFrame(list(zip(list(range(10000)), MSE_list)), columns=["iter", "MSE"])
df2.to_csv("loss.csv", index=None)このコードで行っていることは以下の図のように①、②、③を10000回繰り返して②を差を最小にするようにしています。
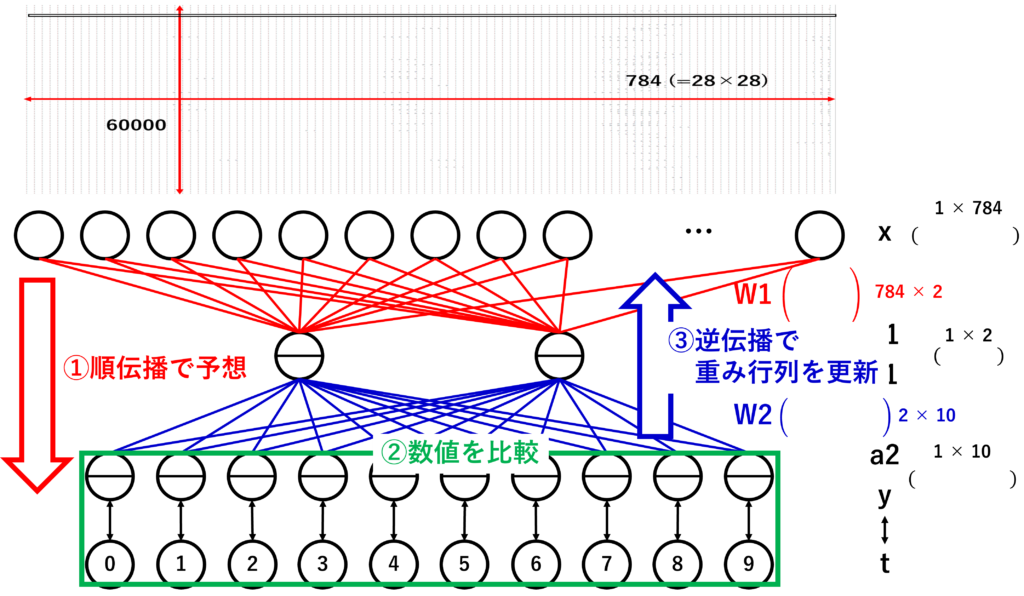
この10000回の更新が終わったら、最後に順伝播を行い、正解の数字を比較して、正解率をお求めています。
結果は約96.5%でした。
自作(本を参考にして改造)にしてはまぁまぁだと思います。
重みと損失関数の更新履歴
では、この結果を使って、どのように精度が上がっていくのか確認してみます。
まず、重みが10000回の更新の中でどう変化するのか見てみます。すべての重みを見るのは大変なので、W2の中でも正解した時のニューロンとハズレの時のニューロンの重み、W1の中で入力層が0にならない重みをグラフ化します。
選択した重みがどれに該当するかは以下の図の赤線、青線になります。青線の中でも点線と実線がありますが、点線がハズレの重み、実線が正解の重みになります。
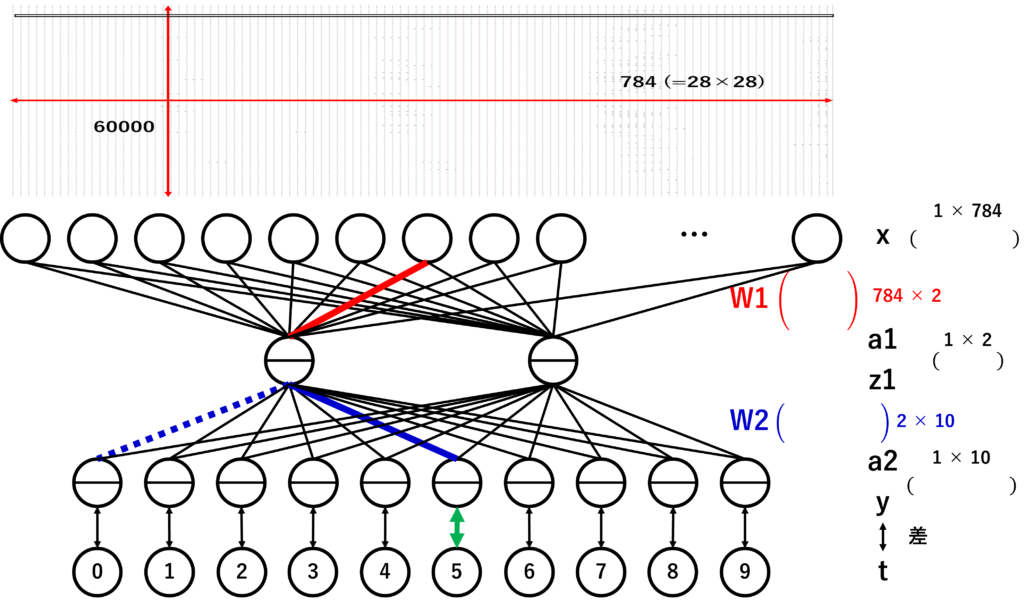
重みの更新履歴
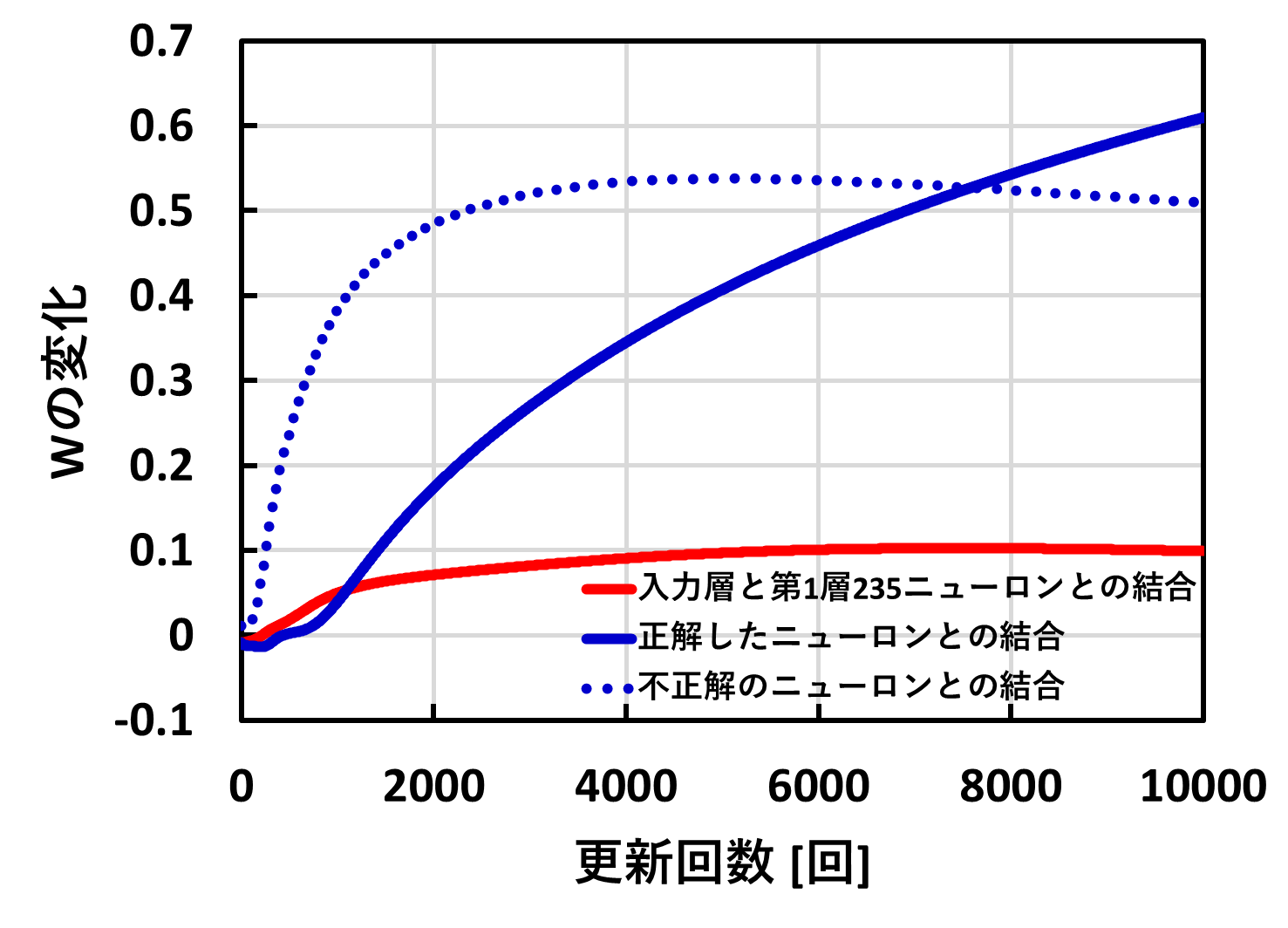
さっそく、重みのグラフになります。
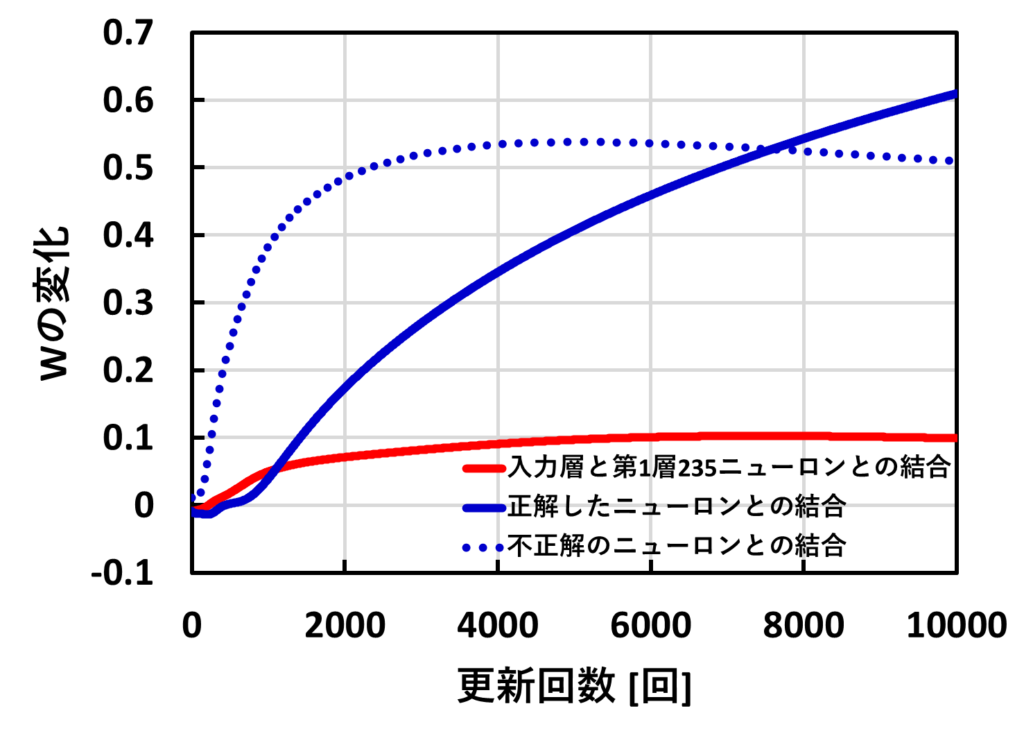
まずは全体的な傾向です。更新回数が増えるごとに重みが増加し、各ニューロン同士の結合が強くなっていることが分かりました。
次に赤線のW1の重みです。青線に比べ重みの増加量が小さいことが分かりました。
最後に、青線のW2の重みです。更新回数が7500回までは不正解(点線)の重みが正解(実線)の重みに比べ大きくなっていることが分かりました。そして、7500回より大きくなると逆転し、正解のの重みの方が大きくなっていることが分かります。
さて、この結果にかんして、考察してみましょう。全体的な増加はAIが徐々に頭がよくなっていることを示しているのではないのでしょうか。ただし、今回は関係があるところしか見ていないので、入力層が0のところなどを見ると、ほとんど変化しないと思われます。その点で荒い考察になります。
赤線を青線に関して、考察したいですが、赤線が青線に比べ小さくなった理由はわかりませんでした。青線の点線と実線に関してもなぜ逆転したのかわかりませんでした。しかし、正解の重みが大きくなったことで、正解のニューロンの結合が強くなり、正解率が増えたのではないのかと考えています。
ん~。難しいですね。パッと考察できる範囲でしてみました。
損失関数の更新履歴
続いて、10000回の更新回数の中で予測した数字と正解の数字の差(損失関数)を追跡してみます。
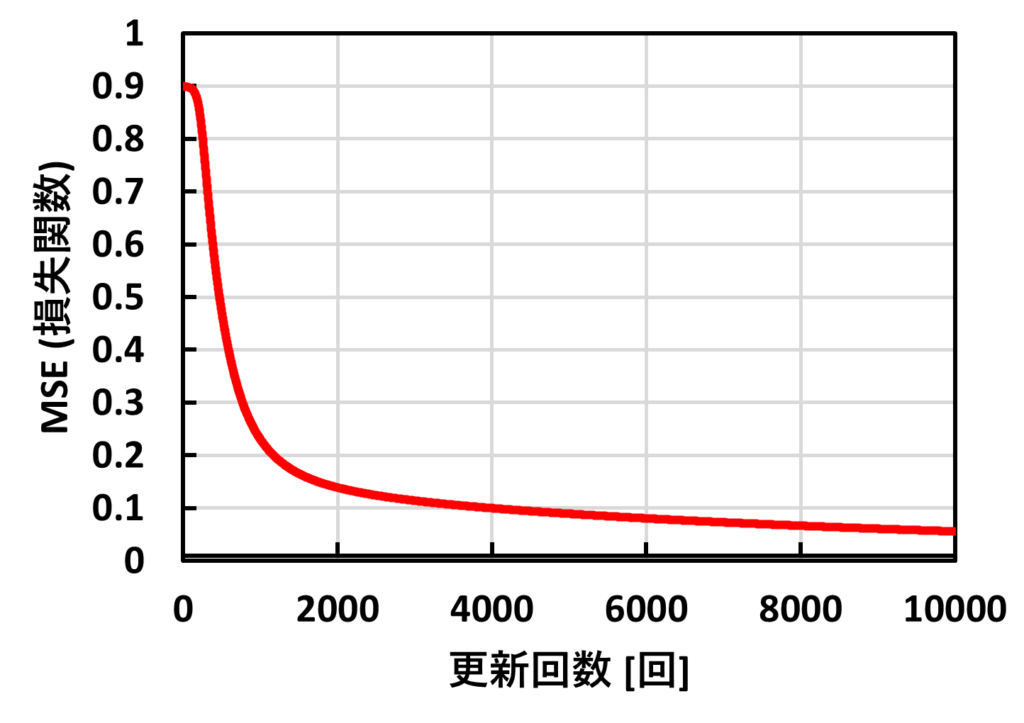
この結果をみると、更新回数を重ねるごとに差が0になっていることがわかります。ということは更新回数が進むと精度がよくなっていることが言えます。
もっと更新回数を増やせば差が小さくなり、正解率がもっと大きくなるのではないかと思いますが、計算時間がとてつもない時間になりそうです。(高性能PCが必要ですね(笑)。)
年末年始で更新回数によって正解率が変化するか確認しました。それが以下の図です。
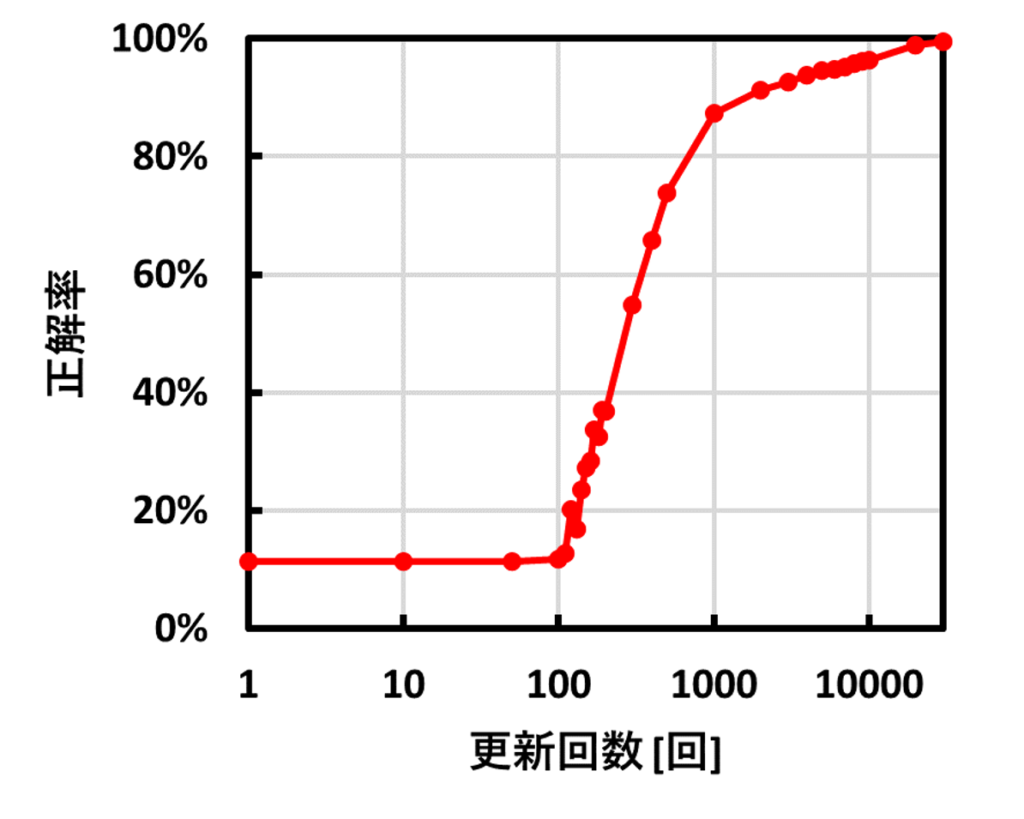
更新回数100回までは正解率はほとんど変化しませんが、100を超えた途端に急激に正解率が良くなり、30000回ほどでほぼ100%に達しています。
最後に
今回まででAIの核である順伝播と逆伝播を調査してみました。次回は精度と計算速度を大きく決める最適化関数について調査してみたいと思います。
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/398737cb.3d026dbe.398737cc.417981d6/?me_id=1213310&item_id=18172266&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F7584%2F9784873117584.jpg%3F_ex%3D240x240&s=240x240&t=picttext)



コメント