逆伝播について調査してみた。(初心者が本とChatGPTを使ってAIを作って研究してみた）

ChatGTP-AI研究開発
2023.12.26

はじめに

これまでChatGPTやネットを使ってAIの数字分類や回帰について調査してきました。

なんとなく、AIでできることや概要が分かるようになってきましたので、次にどうやってAIが動いているのか本とChatGPTを使って調査していきたいと思います。

今回は順伝播と対と為す逆伝播について調査していきたいと思います。

参考にした本は

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装


順伝播の復習

まずは順伝播の復習します。詳しくはこちら。

順伝播は入力されたデータから中間層に伝播し、中間層から出力層に伝播するという流れでした。その際、数学の行列の概念を使って伝播するようすを前回調査しました。

この行列のうち重みを使った行列(今回は重み行列と言います)が適切な値であれば、AIとして優秀なモデルと言えるそうです。

逆伝播を調査してみた

逆伝播の概要

適切な値をやみくもに探しても見つかるわけもありません。そこで出力層の情報を入力層まで伝播させて、適切な値を発見しようという試みが逆伝播のようです。イメージとしては以下の図のようになります。

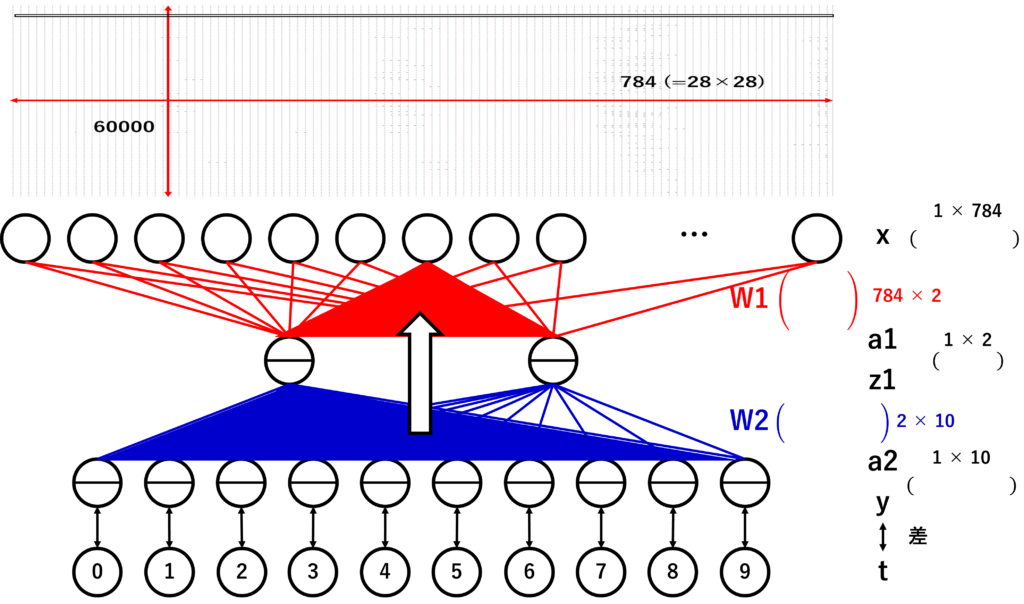
前回の順伝播の逆の流れですね。(前回同様。伝われー)

概要は分かりましたが、実装できるように式を追ってみたいと思います。

順伝播の計算順の復習

まずは前回の順伝播の計算順を復習します。

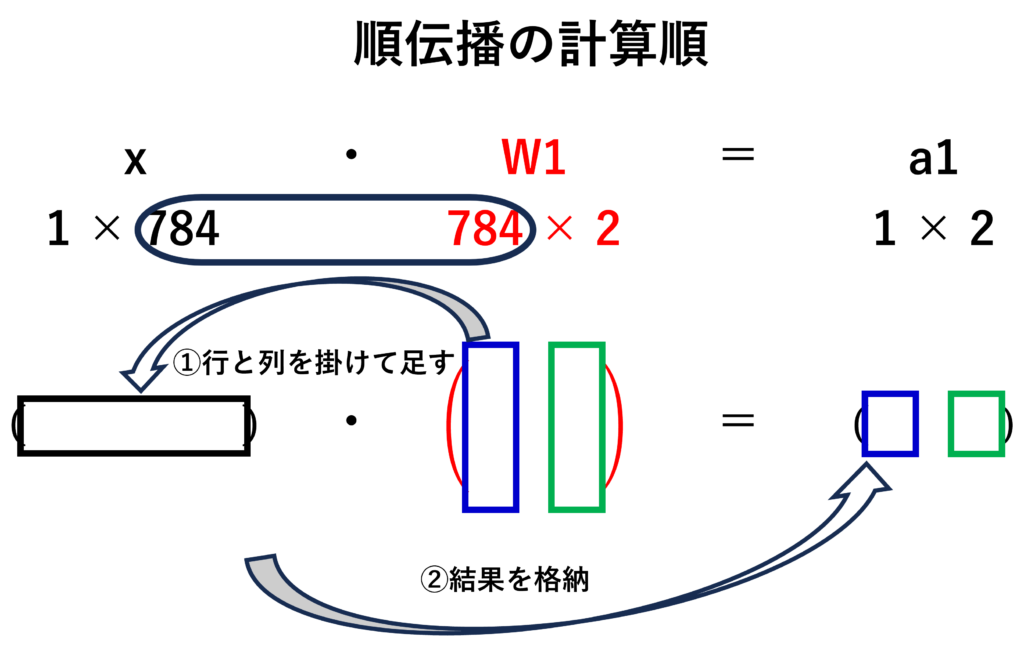
入力層の行列に重み行列を掛け算します。高校や大学で行列の計算に慣れていない人のためにごくごく簡単に説明します。

まず、1×784の意味ですが、1行784列という意味です。Excelを思い出していただければいいと思います。1行目にA~XXX(？)列まで数字があると思ってください。それが行列です。

この1×784の行列に掛け算できる行列は784行ぴったし列は1以上です。上の図の丸横長がそろうようにします。

この2つの行列ができれば掛け算ができますが、普通の掛け算と違って、めんどくさいのですが、あとに準備した行列の1列目(ExcelでいうA列)を最初に用意した1行目に各要素を掛けて足す。その結果を計算結果の1列目に格納します。それをあとに準備した行列の列だけ繰り返します。これが行列の掛け算です。

行列の掛け算は順番が重要になります。右から掛けるか左から掛けるかで結果が変わってきます。順伝播の場合、入力層×重みのように順番に掛けていけば大丈夫です。

逆伝播の計算順

さて、ここからが今回の本題である逆伝播の計算方法です。

逆伝播の計算をするための準備(転置行列)

逆伝播を計算するには逆行列(または転置行列)の概念が必要になります。今回は転置行列をメインに説明します。転置行列は行と列を入れ替えた行列になります。1行目が1列目になり、2行目が2列目になりと具合になる行列です。イメージとしては下の図のようになります。

行と列が変わるので、1×784の行列が784×1行列になっています。この行列の性質として重要なのが、転置する前の行列と転置行列を掛け算をすると1のような行列ができることです。

この転置行列と転置行列の性質を使うことで逆伝播を行うことができるようになります。

逆伝播の計算順

この転置行列を順伝播の式の両辺に入力となる行列の転置行列を掛け算すると重み行列が求めることができ、下の図のようになります。

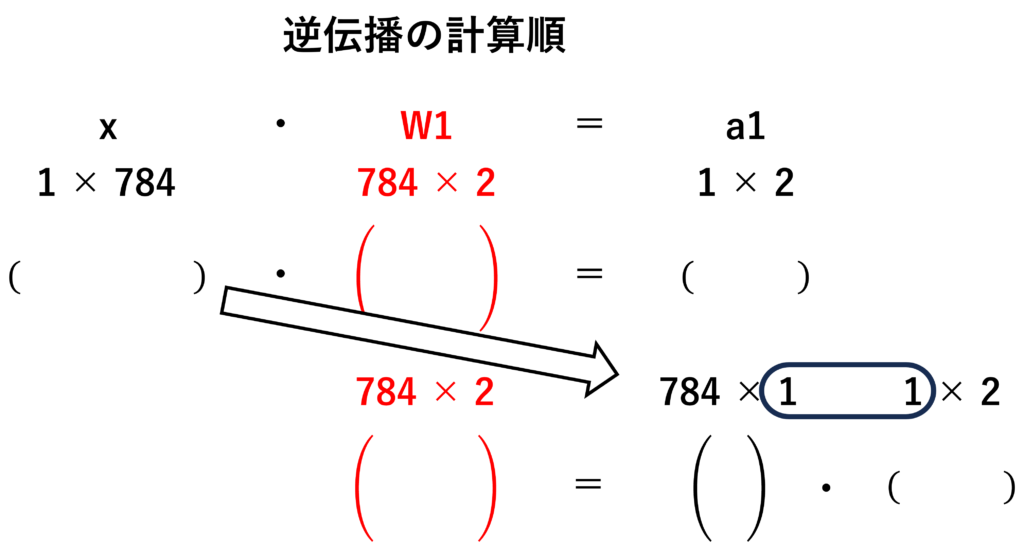
逆伝播の目的は順伝播で出力された行列から重み行列を導き出すことなので、一応上の式で目的は達成です。

これでようやく逆伝播の実装ができそうです。

逆伝播の実装

それでは実装。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical

(x_train, t_train), (x_test, t_test) = mnist.load_data()

x_train = x_train.reshape((x_train.shape[0], -1)).astype('float32') / 255
x_test = x_test.reshape((x_test.shape[0], -1)).astype('float32') / 255
t_train = to_categorical(t_train, 10)
t_test = to_categorical(t_test, 10)
 
input_size = 784
output_size = 10
 
hidden_size = 50
 
weight_init_std = 0.01
 
W1 = weight_init_std * np.random.randn(input_size, hidden_size)
b1 = np.zeros(hidden_size)
W2 = weight_init_std * np.random.randn(hidden_size, output_size)
b2 = np.zeros(output_size)
 
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
 
def softmax(x):
    x = x - np.max(x, axis=-1, keepdims=True)
    return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
 
x = x_train
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)



 #ここから逆伝播の実装
 
 
def sigmoid_grad(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)
 
learning_rate = 0.1
 
t = t_train
dy = (y - t) / x.shape[0]
grad_W2 = np.dot(z1.T, dy)
grad_b2 = np.sum(dy, axis=0)
W2 = W2 - learning_rate * grad_W2
b2 = b2 - learning_rate * grad_b2
 
dz1 = np.dot(dy, W2.T)
da1 = sigmoid_grad(a1) * dz1
grad_W1 = np.dot(x.T, da1)
grad_b1 = np.sum(da1, axis=0)
W1 = W1 - learning_rate * grad_W1
b1 = b1 - learning_rate * grad_b1

前半は前回の順伝播を示しています。後半が今回の逆伝播になります。

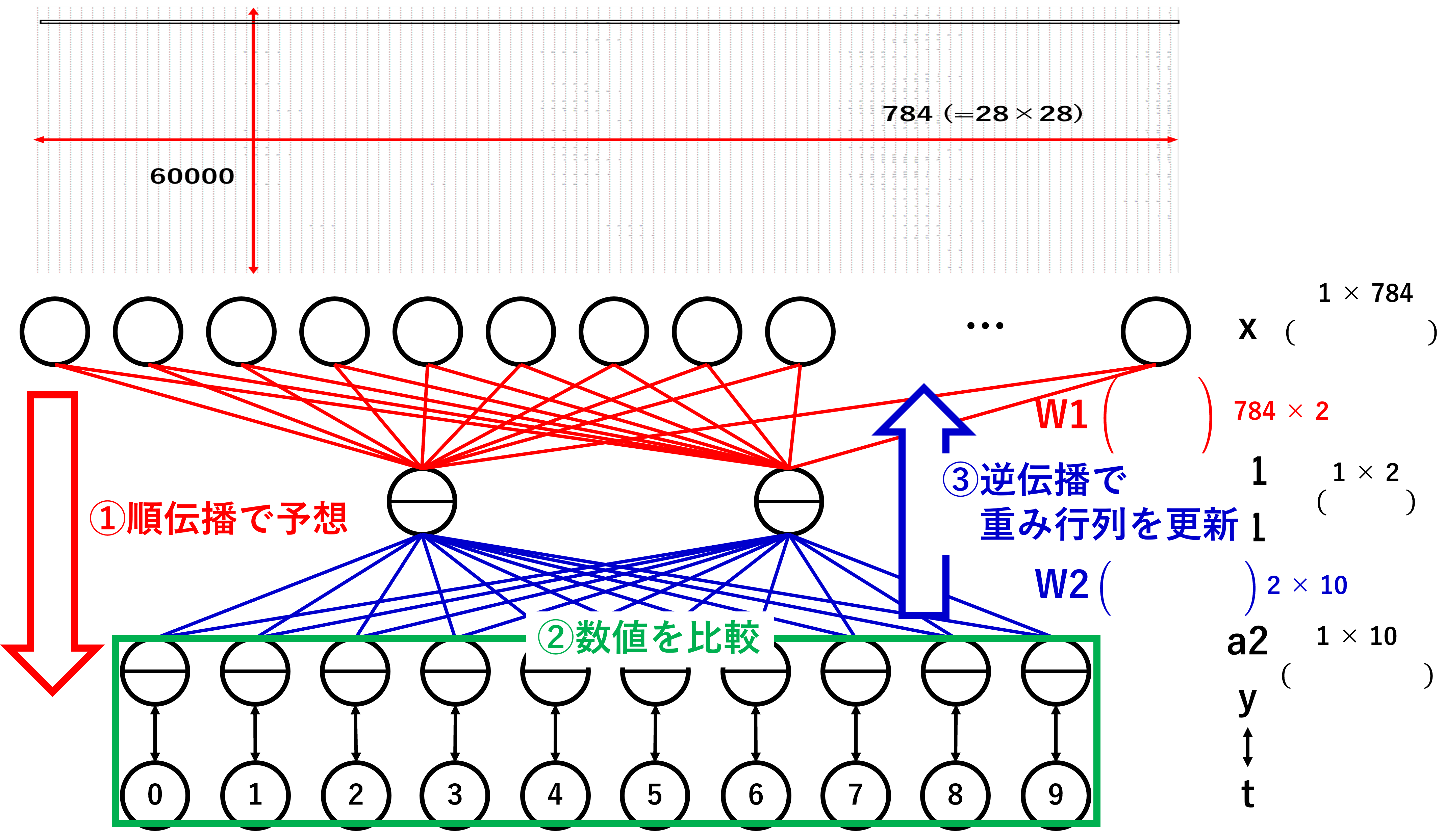
ただ、逆伝播を実装するのには逆伝播誤差法という、順伝播で予測した値と正解となる値を比較してその誤差を最小にしていくという方法が実用的なようなので、本を参考に実装してみました。逆伝播誤差法のイメージとしては以下の図のようになります。

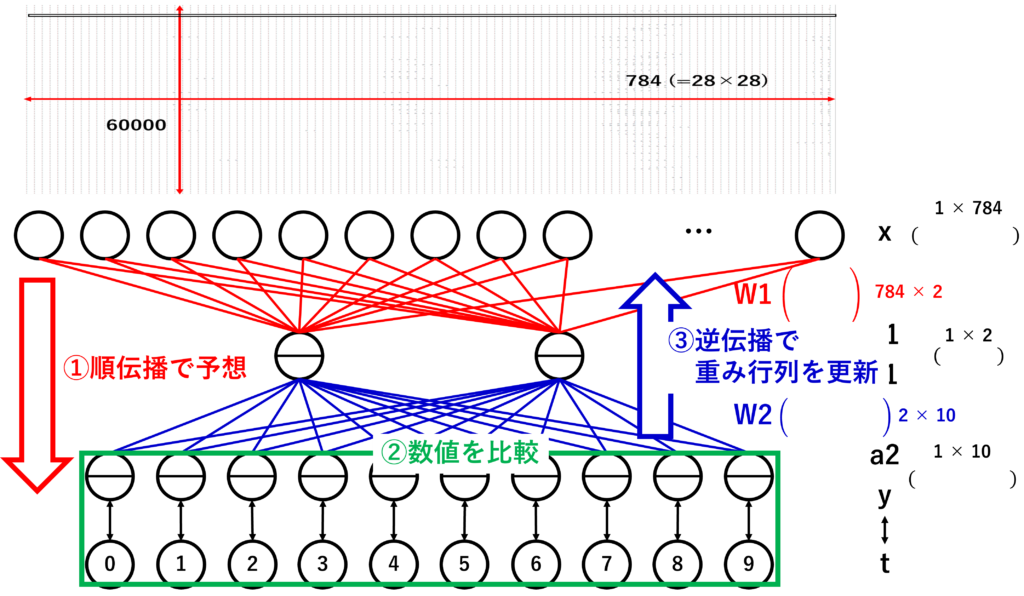
実装の際は順伝播の予測と正解の数値を引き算して誤差を表しています。これを実装したのが以下の行です。

dy = (y - t) / x.shape[0]

このdyを基に逆伝播していきます。順伝播でのyの一つ前は活性化関数なので、活性化関数を計算した後のz1の転置行列を掛け算します。それが以下のコードです。

grad_W2 = np.dot(z1.T, dy)

z1の転置行列をpythonで実装するには.Tとするだけです。さらに転置行列とdyを計算するために行列積を示すnp.dotで計算します。このとき掛ける順番に注意して実装します。

これで重み行列を計算できた！と思いきや逆伝播誤差法の特徴に誤差を最小にするということがあるそうで、単純にこれが重み行列になるのではなく、この計算された行列が更新量となるように重み行列を計算するようです。(これに関しては後日勉強します…)

実際の重み行列の計算は

W2 = W2 - learning_rate * grad_W2

で計算されます。元々の重み行列に先ほどの更新量を引き算して新たな重み行列を作っています。learning_rateは学習率という量で更新量でもどのくらい更新するか決める量のようです。学習率の数値が大きいと大きく更新され、小さいと少なく更新されるようです。

これを入力層まで伝播していき、重み行列を更新し、より精度の高いAIを作っていくようです。ただ、1回の更新では良い精度のAIを作れるのではなく、何十回も何百回も更新して高精度のAIを作っていくようです。

そこで、次回はたくさん更新していみて、精度はよくなるのか、重み行列がどう変化するかを確認していみたいと思います。その結果を使って実際にAIの頭がよくなる様子を見ていきたいと思います。

では、今回はここまで

コメント

タイトルとURLをコピーしました