はじめに
こちらの記事でpythonによるシュレディンガー方程式を紹介しました。行列の扱いが技巧的で感動したことを紹介させていただきました。
ここではプログラミングを行った結果を考察し、プログラミングの妥当性であったり、自分の知識の確認を行っていきたいと思います。
今回は、本来の目的であるポテンシャルの関数の形で波動関数の挙動を調べてみます。今回は4つのポテンシャルの関数で調べます。初めの3つは量子力学を学び始めて扱う関数型です。最後の一つは前回紹介しましたアンモニアの反転振動を扱ってみます。
色々なポテンシャルエネルギー
壁関数型ポテンシャル
では、まずx=0を境にポテンシャルが急激に変化する壁関数型ポテンシャルでの波動関数の挙動を紹介します。ポテンシャル関数を以下のように定義します
$$ V(x) = \begin{cases} 0 & (x < 0) \\ 50 & (x \geq 0) \end{cases} $$上式をコードに反映させると以下のようになります
# potential term
def potential(x):
pot_list = np.empty(len(x))
for i in range(len(x)):
hanntei = x[i]
if hanntei<=0:
pot_list[i] = 0
elif hanntei>0:
pot_list[i] = 50
return pot_list
v_diag = potential(x)イメージはx=0にものすごい高い壁があるような感じです。その壁を超えるような大きなエネルギーがなければ壁の前で存在確率が大きいことが予測されます。では、前回のシュレディンガー方程式を解いてみます。
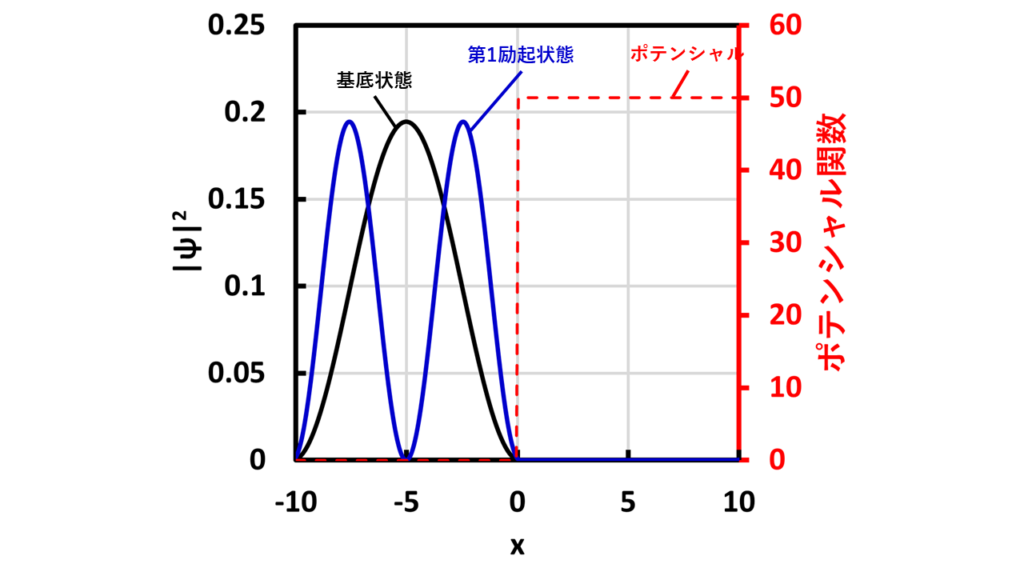
上のグラフはシュレディンガー方程式を解いた結果を示しています。赤線がポテンシャル関数で、黒線が基底状態での波動関数の存在確率、青線が第1励起状態での波動関数の存在確率です。
基底状態の固有エネルギーが約0.05、第1励起状態の固有エネルギーが約0.19です。ポテンシャルエネルギーより十分小さいエネルギーなので予想通り、壁を乗り越えられず壁の前での存在確率が大きくなっています。
階段型ポテンシャル
次にx=0、5を境にポテンシャルが階段状に変化する階段型ポテンシャルの波動関数の挙動を紹介します。ポテンシャル関数を以下のように定義します
$$ V(x) = \begin{cases} 0 & (x < 0) \\ 0.5 & (0 \leq x < 5) \\ 50 & (x \geq 5) \end{cases} $$上式をコードに反映させると以下のようになります
# potential term
def potential(x):
pot_list = np.empty(len(x))
for i in range(len(x)):
hanntei = x[i]
if hanntei<=0:
pot_list[i] = 0
elif hanntei>0 and hanntei<=5:
pot_list[i] = 0.5
elif hanntei>5:
pot_list[i] = 5
return pot_list
v_diag = potential(x)イメージはx=0に小さい壁があり、x=5で大きな壁があるような感じです。大きな壁は乗り越えることができませんが、小さな壁はエネルギーの程度で一部乗り越え、存在確率が滲みだすことが予測されます。では、前回のシュレディンガー方程式を解いてみます。
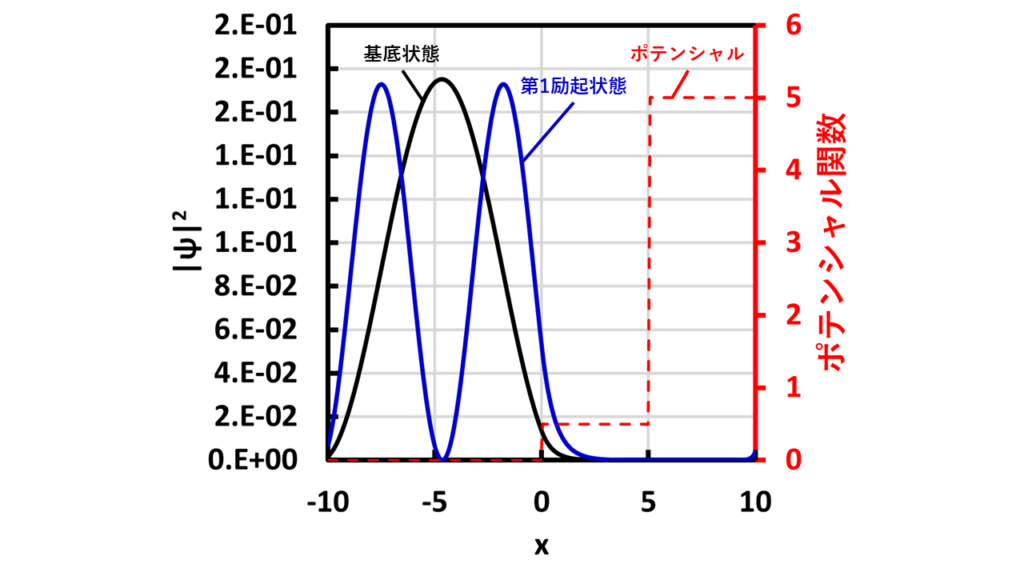
上のグラフはシュレディンガー方程式を解いた結果を示しています。赤線がポテンシャル関数で、黒線が基底状態での波動関数の存在確率、青線が第1励起状態での波動関数の存在確率です。
基底状態の固有エネルギーが約0.04、第1励起状態の固有エネルギーが約0.15です。ポテンシャルエネルギーより小さいエネルギーですが、トンネル効果という現象で一部滲みだしていることがわかります。
調和振動子型ポテンシャル
次からはxが急激に変化する関数ではなく滑らかな関数について紹介します。まず、2次関数型ポテンシャルの波動関数の挙動を紹介します。一般に調和振動子というポテンシャル関数になります。
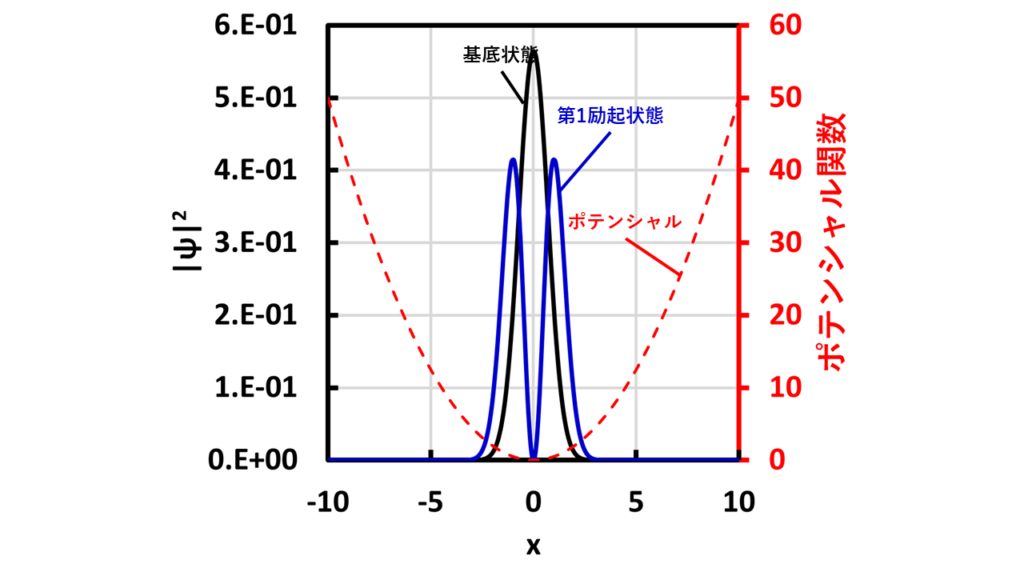
上のグラフはシュレディンガー方程式を解いた結果を示しています。赤線がポテンシャル関数で、黒線が基底状態での波動関数の存在確率、青線が第1励起状態での波動関数の存在確率です。
基底状態の固有エネルギーが約0.5、第1励起状態の固有エネルギーが約1.5、第2励起状態の固有エネルギーが2.5、3.49、4.49、・・・と各固有エネルギーの差が1と等間隔になっていることがわかりました。また、ポテンシャルエネルギーより小さいエネルギーですが、トンネル効果という現象で一部滲みだしていることもわかります。
反転振動型のポテンシャル
さて、ここまでは教科書レベルのポテンシャル関数でした。前回の記事で反転振動を取り扱いました。反転振動のポテンシャル関数型は4次関数の形をしています。というのもアンモニアのような三角錐が安定構造です。また、その三角錐をひっくり返した三角錐構造も安定構造です。どちらの三角錐構造がたくさん存在しているかという判別は非常に大変です。その理由は状態の重ね合わせなのですが、直感的に理解するには三角錐構造のひっくり返りの速度が非常に速い(1秒で1000000000回ひっくり返りかえる)からともいえます。今回のポテンシャルエネルギーとどう関わってくるでしょうか考えてみましょう。三角錐構造Aから三角錐構造Bへ反転するとします。三角錐構造AとBは対称的なので同じポテンシャルエネルギーを持っています。そして、安定構造なので最小値になります。さて、三角錐構造AとBの途中はどうなっているでしょうか?答えはすべての原子が同一平面上に存在するときです。同一平面に原子が存在すると、原子同士が近づいてポテンシャルエネルギーが非常に大きくなります。動きとしては三角錐構造A、同一平面、三角錐構造Bに変化します。そして、ポテンシャルエネルギーは最小値、極大値、最小値となっています。滑らかに変化すると仮定するとおおよそ4次関数型のポテンシャルになります。それでは、4次関数型ポテンシャルの波動関数の挙動を紹介します。

上のグラフはシュレディンガー方程式を解いた結果を示しています。赤線がポテンシャル関数で、黒線が基底状態での波動関数の存在確率、青線が第1励起状態での波動関数の存在確率です。
赤線のポテンシャルエネルギーの最小値の2か所に黒線と青線の波動関数のピークがあります。しかも、波動関数のピークはポテンシャルエネルギーの最小値の片方ずつあります。また、上図では基底状態と第1励起状態と分けていますが、固有エネルギーはほとんど差がありません。なので、2つの状態はほぼ同じ状態をしているということがわかります。これは前述した三角錐が反転しても同じ構造が安定ということを示しています。では、ここから反転振動の周期を求めたいところですが…。内容が内容なので別の記事にしたいと思います。イメージとしては黒線から青線に移動。青線から黒線に移動というのを繰り返しの運動しており、その振動数がおおよそ(固有エネルギーの差) / (ディラック定数)程度になります。
最後に
今回は以上になります。内容がハードでしたが、プログラミングしてみた結果を考察してみました。定量的な議論はやや難しいですが、定性的な議論には一部使えそうです。また、量子力学を学び始めた方は学んだ結果を自分ので手で確認することができると思います。
2023/08/08 J.A


コメント