はじめに
これまでChatGPTやネットを使ってAIの数字分類や回帰について調査してきました。
なんとなく、AIでできることや概要が分かるようになってきましたので、次にどうやってAIが動いているのか本とChatGPTを使って調査していきたいと思います。
今回はAIの精度と計算速度を決める最適化関数について調べてみました。やや数学的な内容を含むので、難しくなるかもしれませんが頑張っていきます。
参考にした本は
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
最適化関数について調べてみた
最適化について
最適化とはwikiより
数学的に記述された制約の範囲内で、目的とする関数値を最大化、あるいは最小化する解を求めること。
とあります。これまで勉強したことと合わせると順伝播で予測した値と正解の値の差を最小化するようにしていくことになりそうです。
そして、その最小化するのにいくつかの方法があり、こちらやこちらのような様々な種類、計算手法(アルゴリズム)があるようです。
詳しくは他の方におまかせして、私はこれらアルゴリズムを実装して、計算精度が変化するか見ていきたいと思います。
実装
各最適化関数の式や実装に関しては冒頭の本を参考にしています。
私はもっと簡単に2次関数の最小値を各最適化関数で求めていきたいと思います。
良い最適化関数というのは2次関数に沿って最小値を求めていくことだと思っています。この仮定で実装していきたいと思います。
import numpy as np
def f(x):
return x**2 / 20.0
def df(x):
h = 1e-7
dfdx = (f(x+h) - f(x-h))/h
return x / 10.0
N = 1000
lr = 0.01
start = 5
"""確率的勾配降下法(Stochastic Gradient Descent)"""
init_pos = start
lr = lr
SGD_list = []
for _ in range(N):
init_pos = init_pos - lr*df(init_pos)
SGD_list.append(init_pos)
"""Momentum SGD"""
init_pos = start
lr = lr
momentum=0.9
v = None
MSGD_list = []
v_list = []
for _ in range(N):
if v == None:
v = np.zeros_like(init_pos)
v = momentum*v - lr*df(init_pos)
init_pos = init_pos + v
MSGD_list.append(init_pos)
v_list.append(v)
"""Nesterov's Accelerated Gradient"""
init_pos = start
lr = lr
momentum = 0.9
w = None
NA_list = []
w_list = []
for _ in range(N):
if w == None:
w = np.zeros_like(init_pos)
init_pos = init_pos + (momentum**2) * w
init_pos = init_pos - (1 + momentum) * lr * df(init_pos)
w = w*momentum
w = w - lr*df(init_pos)
NA_list.append(init_pos)
w_list.append(w)
"""AdaGrad"""
init_pos = start
lr = lr
h = None
AG_list = []
h_list = []
for _ in range(N):
if h == None:
h = np.zeros_like(init_pos)
h = h + df(init_pos) ** 2
init_pos = init_pos - lr*df(init_pos) / (np.sqrt(h) + 1e-7)
AG_list.append(init_pos)
h_list.append(h)
"""RMSprop"""
init_pos = start
lr = lr
decay_rate = 0.99
u = None
RMS_list = []
u_list = []
for _ in range(N):
if u == None:
u = np.zeros_like(init_pos)
u = u*decay_rate
u = u + (1 - decay_rate)*df(init_pos)**2
init_pos = init_pos - lr*df(init_pos) / (np.sqrt(u) + 1e-7)
RMS_list.append(init_pos)
u_list.append(u)
"""Adam"""
init_pos = start
lr = lr
beta1 = 0.9
beta2 = 0.999
iteration = 0
m = None
n = None
Adam_list = []
m_list = []
n_list = []
for _ in range(N):
if m == None:
m = np.zeros_like(init_pos)
n = np.zeros_like(init_pos)
iteration += 1
lr_t = lr * np.sqrt(1.0 - beta2**iteration) / (1.0 - beta1**iteration)
m = m + (1 - beta1) * (df(init_pos) - m)
n = n + (1 - beta2) * (df(init_pos)**2 - n)
init_pos = init_pos - lr_t * m / (np.sqrt(n) + 1e-7)
Adam_list.append(init_pos)
m_list.append(m)
n_list.append(n)
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.01)
x2 = np.linspace(-10, 0, N)
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.plot(x, f(x), linewidth=5)
ax1.plot(x2, SGD_list, '-', color="red", label="SGD")
ax1.plot(x2, MSGD_list, '-', color="yellow", label="MSGD")
ax1.plot(x2, NA_list, '-', color="purple", label="NA")
ax1.plot(x2, AG_list, '-', color="green", label="AG")
ax1.plot(x2, RMS_list, '-', color="blue", label="RMS")
ax1.plot(x2, Adam_list, '-', color="orange", label="Adam")
plt.legend()
ax2 = ax1.twinx()
ax2.plot(x2, v_list, '--', color="yellow", label="MSGD_v")
ax2.plot(x2, w_list, '--', color="purple", label="NA_v")
#ax2.plot(x2, h_list, '--', color="green", label="AG_v")
ax2.plot(x2, u_list, '--', color="blue", label="RMS_v")
ax2.plot(x2, m_list, '--', color="orange", label="Adam_v")
ax2.plot(x2, n_list, '--', color="black", label="Adam_v2")
plt.legend()
plt.show()コードについてはほぼ本をパク…、参考にしていますので、詳しく知りたい方は本を見てください。
各最適化関数の比較
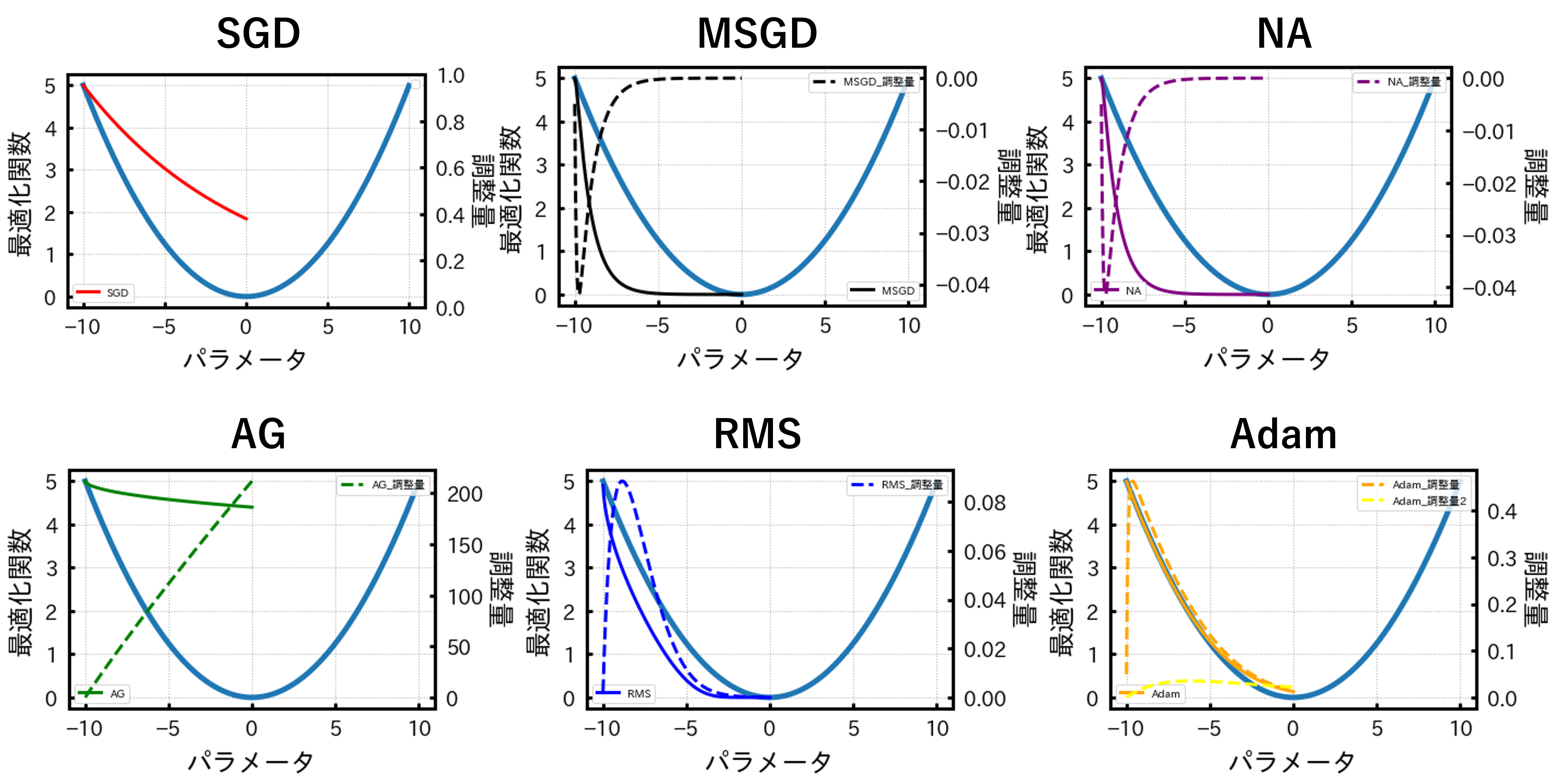
さて、2次関数と各最適化関数から得られる結果をプロットすると以下の図のようになります。
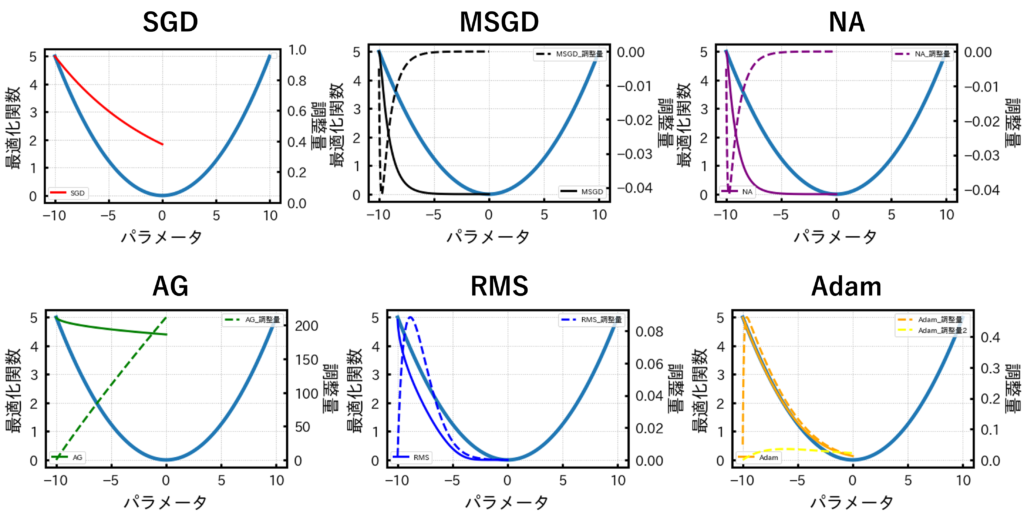
各グラフに共通する双曲線が2次関数です。また、各グラフの色付きの実線が最適化関数で、点線が調整量のようなものになります。
精度のいい最適化関数は2次関数と色付きの実線が一致することでしたのでこの中ではAdamという方法が最も精度が良いということになりますね。
最後に
最適化関数で精度が変わることが分かりました。今後の研究などでは最適化関数を変えて試してみたいと思います。今のところはAdamでいいのかな~。
とりあえず、AIの根幹である部分を勉強してみました。次は勉強したことをいろいろ応用していきたいと思います。

コメント