はじめに
前回の記事では「重み」を直観的な方法で説明しました。今回はその「重み」を数学的に定義して、物理やAIに応用できるようにしていきます。参考書に載っていることに近いかもしれませんが、私なりのイメージや理解の仕方で説明したいと思います。「数学的に定義する」ということなので、どうしても同じ内容になってしまうことがあります。しかし、”覚え方”などはあまり本には書かれていないと思うので、そういった部分を参考にしてもらえるといいかもしれません。
ベクトルと内積
ベクトルの拡張
前回の復習
まず、前回の復習です。前回は2つのベクトルを定義しました。1つ目は「人生要因縦ベクトル」、2つ目は「重み横ベクトル」です。式にすると
$$ \left( \begin{array}{c} お金 \\ 人脈 \\ 趣味 \\ \vdots \end{array} \right) $$
$$ ( 30, 20, 50, \ldots ) $$
です。要因を縦に並べた”ベクトル”と重みを横に並べた”ベクトル”になります。
ベクトルの拡張
ここでベクトルの定義を拡張しましょう。高校でベクトルを習うと「向き」が重要視されます。もちろん重要な概念ですが、数学で扱おうとするとやや不便です。そこで、向きを座標で表すという手法を採用します。下図を見てもらうとイメージがつきやすいです。

原点Oからx方向に1、y方向に1進んだベクトルが赤線、x方向に-3、y方向に2進んだベクトルは青線になります。矢印は直観的にすごく分かりやすいです。赤線、青線が進んだ方向が簡単に理解することができます。
しかし、コンピュータは矢印ではなく数値の方が理解しやすいです。急にコンピュータという言葉がでてきましたが、仕方がないと受け入れてください。数学とコンピュータは切っても切れない関係にあります。
矢印を数値に変換すると、赤線は(1, 1)、青線は(-3, 2)となります。上の図では縦に並べていますが、表記としてはどちらでも大丈夫です。ここで重要なのは矢印が数字に変換されたということです。矢印も数字もどうちらも”ベクトル”と呼びます
ベクトルの次元
これができると、n次元まで拡張できます。今までは2次元(x軸とy軸)のベクトルでしたが、3次元、4次元、…と次元が増やしていくことができます。よく2次元は平面、3次元は立体、4次元は空間と時間と聞きます。これも間違えではありませんが、きちんと理解するには基底ベクトルを知らないといけないのですが、ここでは(1,1,…)とベクトルを数値化したものの括弧の中の個数と理解してください。
例えば、
(1, 1)は2次元
(1, 2, 3)は3次元
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)は10次元
です。括弧の中の個数がn個ならn次元になります。
ここまではベクトルの拡張と次元についてでした。次にこのベクトルを「重み」と関連付けさせます。
内積
前回、人生を重み付けすると以下のような式になることを示しました。
$$ 人生 = 30 × お金 + 20 × 人脈 + 50 × 趣味 + … $$
「重み付け」というのは掛けてすべて足すという処理でした。
これをベクトルで表現させるためには内積という処理を行います。上の式を内積を使って表現しなおすと
$$ 人生 = ( 30, 20, 50, \ldots ) \cdot \left( \begin{array}{c} お金 \\ 人脈 \\ 趣味 \\ \vdots \end{array} \right) $$
となります。書き方を変えただけで内容は全く同じです。内積の記号は「・」です。読み方はドットと呼びます。計算の仕方は下の図のようになります。
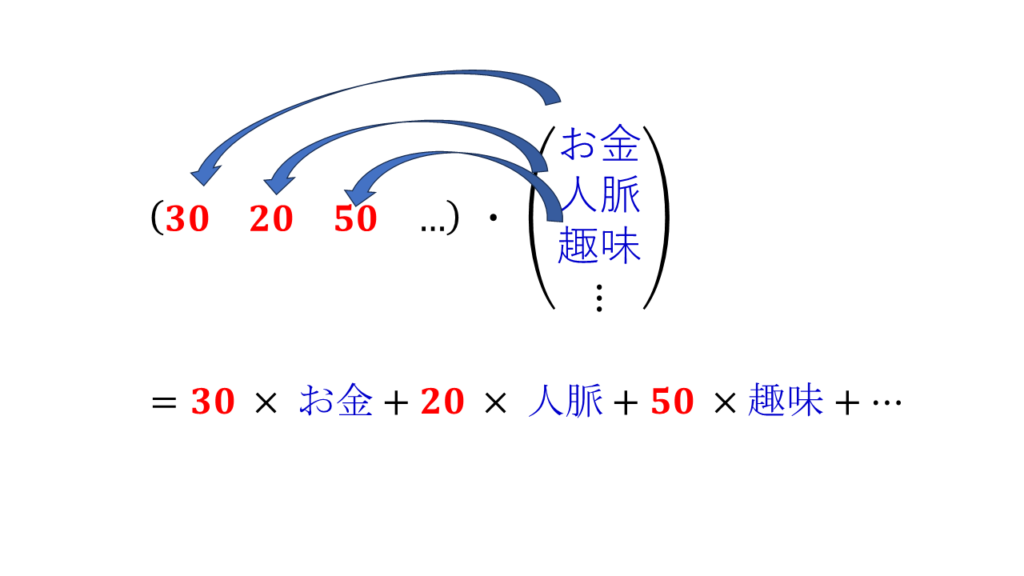
やり方としては図の通りなのですが、私は右手の指を縦ベクトルに合わせて、内側に90°回転して掛けて足すという覚え方をしています。逆の場合縦ベクトルになりうる掛け算に右手の指を合わせて外側に90°回転させてます。覚え方はこのような感じです(笑)。
これが内積です。横に長い式が縦ベクトルと横ベクトルに分けることができるようになりました。だいぶ(コンピュータにとって)扱いやすくなりました。しかし、人が書くとなったらこれも面倒くさい。そこで、縦ベクトルと横ベクトルを文字で置き換えてます。
$$ \boldsymbol{A} = \left( \begin{array}{c} お金 \\ 人脈 \\ 趣味 \\ \vdots \end{array} \right) $$
$$ \boldsymbol{W} = ( 30, 20, 50, \ldots ) $$
とします。ただし、文字は太文字で表します。太文字はベクトルであると意識するためです。内積は
$$ 人生 = \boldsymbol{W} \cdot \boldsymbol{A} $$
と書けます。注意点として、人生は1次元の値なので、横ベクトル・縦ベクトルの順番にしなければなりません。もし、逆順に書いてしまうと、人生は多次元になります(実は多次元の方が正しい!?)。
これで、物理やAIなどの説明がしやすくなりました。もし、「重み」と聞いてわからなくなったら本記事に戻って理解しなしましょう。


コメント